무브

오르비

아톰

내 태그

내 태그 설정

입시
학습
생활
클럽
직업·취업
Epioptimus
Centurion

에라둔 [568834] · MS 2015 (수정됨) · 쪽지

2024-09-27 22:18:15
조회수 2,191

[에라둔] 역학 문항에서의 미래와 과거

게시글 주소: https://susiapply.orbi.kr/00069303116



계산적으로 중요한 내용들은 아니고 그냥 편히 읽으시면 될법한 내용들입니다.





역학 문항을 풀다 보면 여러가지 상황을 마주하게 되는데


종종 동일한 카테고리를 마주하게 됩니다.


이번에 다룰 내용은 어찌보면은 상대속도와 조금 관련이 있을 수 있습니다만 일단 접어두고.


아래 문항들의 공통점이 무엇일까요?



20230618




20210911




20130920



세 문항의 공통점은 두 물체가 모든 지점에 대하여 운동 방향, 속력 모든것이 동일한 상황들입니다.


이전에 저도 문항 출제를 할 때 위와 같은 상황을 이용하여 문항 출제롤 하곤 했는데


위와 같은 문항을 출제하면 참 좋은게 v-t그래프를 옆으로만 삭 밀어주면 되기 때문에

검토하기가 수월해서 즐겨냈었던 기억이 어렴풋이 납니다.


거두절미하고


어떻게 보면 위와 같은 문항들은 상대속도를 활용할만한 문항들 중에서도 특수한 케이스라고 생각을 하는데


저같은 경우에는 두 물체에 대하여 가상의 시간차 t를 가정하고 문제 풀이를 하는것을 선호합니다.


뿐만 아니라, 시간차 t가 난다고 생각하고 문항을 바라보면 좀더 문제 상황을 직관적으로 파악하기도 좋지요.



예를 들어 위 문항의 경우엔 B의 2초 뒤 모습이 A라고 생각하면서 풀면 문제 풀이가 아마 수월하겠죠.

일단 ㄱ이 바로 나올것이며

2초뒤 B가 정지할테니 평균속력 2라는 점에서 v=4가 바로 나올것이며

dv=4인동안의 시간이 2초니 가속도가 2인것도 술술 나올것입니다.



20210911


마찬가지로 위 문항도 B가 t초뒤의 A모습이라고 가정한다면 3vt=L이 나올것이며

우리는 자연스레 A가 p에서 q까지 이동하는데 걸리는 시간이 t라고 할것이기에

평균 속력 공식을 이용하여 1.5vt=0.5L과 같이 문항들이 순둥순둥하게 풀릴것입니다.



위와같이 동일한 경로, 운동 상황을 공유하는 문항의 경우에는 결국엔 대부분 문항에서 요구하는것은

두 상황에 대한 연립일것이며, 이 연립과정이 가감의 과정이기 떄문에


사실 t로 두고 문항을 풀면 쉽게 풀리는 경우가 많습니다.



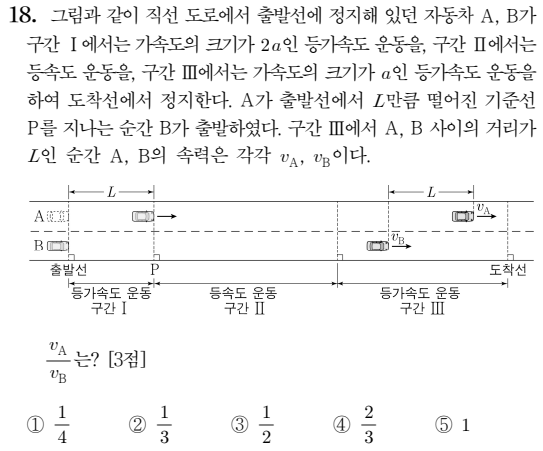
20230618


위 문항의 경우에도 마찬가지로 역시 B의 t후 모습이 A라 생각하고 풀면 풀기가 수월할것입니다.


등가속도 운동 구간 I에서의 가속도를 2a라 하면 (0+2at)t/2=att=L이 나올것이며


이후 vb인 B가 시간 t 후 속력이 va가 된다고 하면 자연스레 (va+vb)/2 * t = L이 나오게 될것입니다.

그리고 구간 3에서 시간 t동안 속력이 변하였는데 이것이 va-vb일지 vb-va일지는 잘 모르겠습니다.


사실 시간 t라는 차이를 생각해보면 B가 출발할 때 이미 가속된 A가 있기에 거리차가 L보다 벌어질텐데

다시 L로 감소했다는 포인트를 보면 아마 가속도가 감소했음을 알기 수월하겠지요.


그러한 이유로 (va+vb)=2L/t,  (vb-va)=at=L/t


va+vb : vb-va = 2:1,   2vb-2va = va+vb, 3va=vb, va:vb=1:3 이 나오게 될것입니다.




저같은 경우에는 두 물체가 동일한 경로를 운동하면 습관적으로 동일한 운동까지 하는지를 체크합니다.


아마 위와같은 유형들을 깔끔하게 푸시는 분들이라면 위의 개념을 숙지한 상태에서

그 이상은 본인의 직관, 암산 등으로 인한 최적화 정도의 차이만이 존재할것입니다.


만약, 위와 같은 수식적 풀이가 다소 어렵다면 그냥 모든 시간 영역을 t미지수로 두고 풀어보시거나


vt 그래프를 정성스럽게 그려보시는것을 권장드립니다.


아마 그래프를 그리시다 보면 자연스레 평행사변형과 친해지게 될겁니다.



 

0 XDK (+0)

  1. 유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.

에라둔 [568834]

쪽지 보내기

글쓰기
오르비 1361602번째 회원 가입
ddna
1,422,072 건의 게시물이
블록체인에 디지털 공증되었습니다.
901,751
497,321
22,267
574
159

오늘의 추천 글

2026 수능D - 335

오르비 플레이

오르비 RARE

오르비 과외시장
Move
our corporate site
Orbi Class
on-line classes
Atom
educational books & resources
Gae9
humor and fun

© 2000-2024 Move Inc.

orbisoptimus (v17-7e2515)